AGI到底離我們還有多遠?在ChatGPT引發的新一輪AI爆發之後,一部分研究者指出,大語言模型具備通過觀察進行因果歸納的能力,但缺乏自己主動推理新的因果場景的能力。相比於持樂觀預測的觀點,這意味著AGI仍然是一個復雜而遙遠的目標。一直以來,AI社區內有一種觀點:神經網絡的學習過程可能就隻是對數據集的壓縮。
近日,伯克利和香港大學的馬毅教授領導的一個研究團隊給出自己的最新研究結果:包括 GPT-4 在內的當前 AI 系統所做的正是壓縮。
通過新提出的深度網絡架構 CRATE,他們通過數學方式驗證這一點。
而更值得註意的是,CRATE 是一種白盒 Transformer,其不僅能在幾乎所有任務上與黑盒 Transformer 相媲美,而且還具備非常出色的可解釋性。
基於此,馬毅教授還在 Twitter 上分享一個有趣的見解:既然當前的 AI 隻是在壓縮數據,那麼就隻能學習到數據中的相關性 / 分佈,所以就並不真正具備因果或邏輯推理或抽象思考能力。因此,當今的 AI 還算不是 AGI,即便近年來在處理和建模大量高維和多模態數據方面,深度學習在實驗中取得巨大的成功。
但很大程度上,這種成功可以歸功於深度網絡能有效學習數據分佈中可壓縮的低維結構,並將該分佈轉換為簡約的(即緊湊且結構化的)表征。這樣的表征可用於幫助許多下遊任務,比如視覺、分類、識別和分割、生成。
表征學習是通過壓縮式編碼和解碼實現的
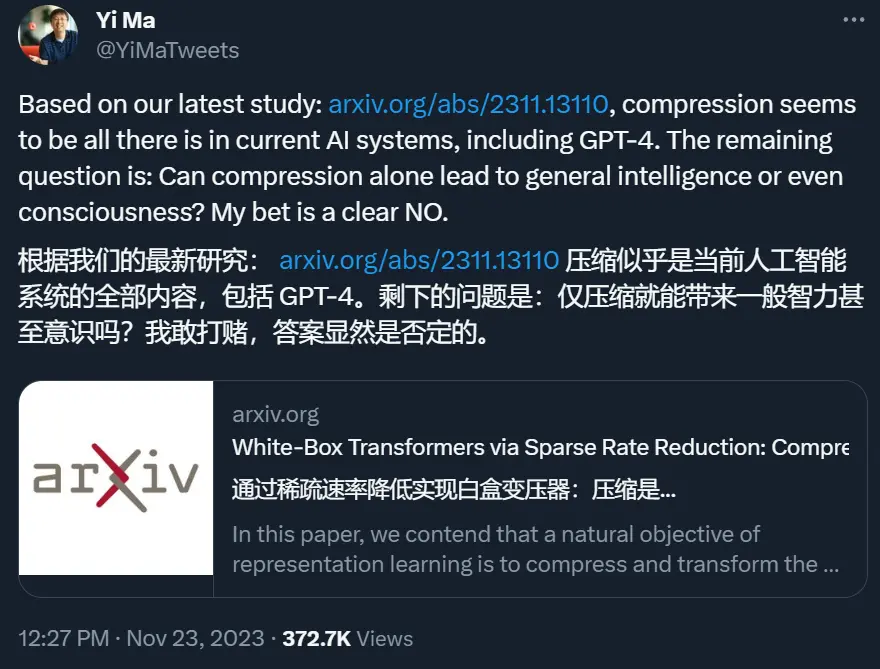
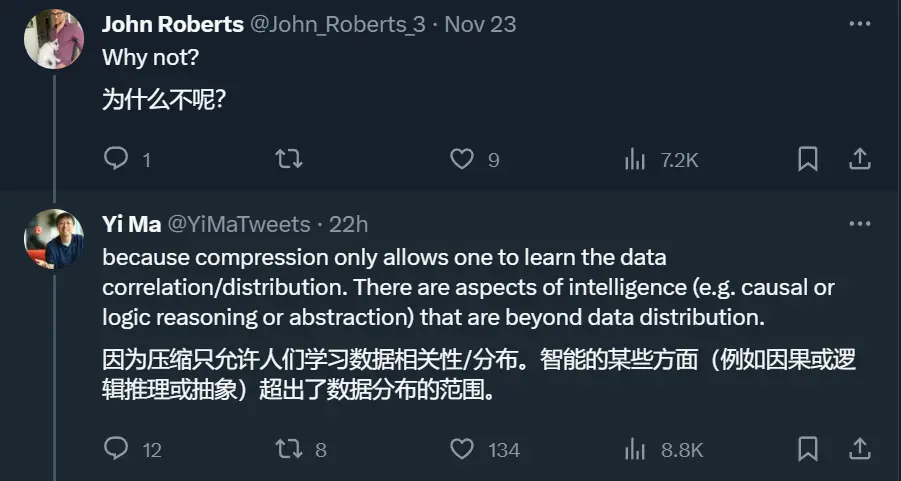
為更形式化地表述這些實踐背後的共同問題,我們可以將給定數據集的樣本看作是高維空間 ?^D 中的隨機向量 x。
通常來說,x 的分佈具有比所在空間低得多的內在維度。一般來說,學習某個表征通常是指學習一個連續的映射關系,如 f (?),其可將 x 變換成另一個空間 ?^d(通常是低維空間)中的所謂特征向量 z。人們希望通過這樣一種映射:
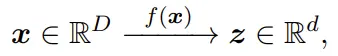
能以一種緊湊且結構化的方式找到 x 的低維內在結構並使用 z 來表示它,然後借此幫助分類或生成等後續任務。特征 z 可被視為原始數據 x 的(學習到的)緊湊編碼,因此映射 f 也稱為編碼器。
這樣一來,表征學習的基礎問題(也即這份研究關註的核心問題)便成:
為衡量表征的優劣,有什麼有數學原理保證且有效的衡量方法?
從概念上講,表征 z 的質量取決於它為後續任務找到 x 的最相關和充分信息的程度以及它表示該信息的效率。
長期以來,人們都相信:所學習到的特征的“充分性”和“優良度”應當根據具體任務而定義。舉個例子,在分類問題中,z 隻需足以用於預測類別標簽 y 即可。
為理解深度學習或深度網絡在這種類型的表征學習中的作用,Tishby and Zaslavsky (2015) 在論文《Deep learning and the information bottleneck principle》中提出信息瓶頸框架,其提出:衡量特征優良度的一種方法是最大化 z 和 y 之間的互信息,同時最小化 z 和 x 之間的互信息。
然而,近年來普遍通行的做法是首先預訓練一個大型深度神經網絡(有些時候也被稱為基礎模型)來學習與任務無關的表征。之後再針對多個具體任務對學習到的表征進行微調。研究表明這種方法能有效且高效地處理許多不同數據模態的實踐任務。
請註意,這裡的表征學習與針對特定任務的表征學習非常不同。對於針對特定任務的表征學習,z 隻需能預測出特定的 y 就足夠。在與任務無關的情況下,所學到的表征 z 需要編碼幾乎所有與數據 x 的分佈有關的關鍵信息。也就是說,所學習到的表征 z 不僅是 x 的內在結構的更緊湊和結構化表征,而且還能以一定的可信度恢復出 x。
因此,在與任務無關的情況下,人們自然會問:對於學習到的(特征)表征,一個衡量其優良度的有原理保證的度量應該是什麼?
研究者認為,一種有效方法(可能是唯一方法)是:為驗證表征 z 是否已經編碼有關 x 的足夠信息,可以看通過如下(逆)映射(也被稱為解碼器或生成器)能從 z 多好地恢復出 x:
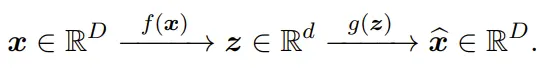
由於編碼器 f 通常是有損壓縮,因此我們不應期望其逆映射能精確地恢復出 x,而是會恢復出一個近似
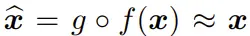
我們通常會尋找最優的編碼和解碼映射,使得解碼得到的
與 x 最接近 —— 無論是樣本方面(例如,通過最小化預期均方誤差)還是在寬松的分佈意義上。
研究者將上述這個過程稱為壓縮式編碼和解碼或壓縮式自動編碼。這一思想與自動編碼器的原始目標高度兼容,而自動編碼器則可被看作是經典的主成分分析泛化用於 x 有線性的低維結構的情況。
過去十一年來,大量實驗已經清楚地表明:深度網絡能夠非常有效地建模非線性編碼和解碼映射。
深度學習的幾乎所有應用都依賴於實現這樣的編碼或解碼方案,其方式是部分或完全地學習 f 或 g,當然它們可以分開或一起學習。
盡管從概念上講,解碼器 g 應該是編碼器 f 的“逆”映射,但在實踐中,我們一直不清楚編碼器和解碼器的架構有何關聯。在許多案例中,解碼器的架構設計與編碼器的關聯不大,通常是通過實驗測試和消融實驗選取的。
可以想見,一個優秀的表征學習理論框架應能清楚地揭示編碼器和解碼器架構之間的關系。而這正是這項研究希望達成的目標。
研究者總結之前提出的相關方法,並將其分成以下幾種情況:
通過壓縮打開現代深度網絡的黑盒。
Transformer 模型和壓縮。
去噪擴散模型和壓縮。
促進低維度的度量:稀疏性和率下降。
展開優化:一個用於網絡解釋和設計的統一范式。
詳情參看原論文。
這項研究的目標和貢獻
他們搭建理論和實踐之間的橋梁。為此,這項研究提出一個更加完整和統一的框架。
一方面,這個新框架能對基於深度網絡的許多看似不同的方法提供統一的理解,包括壓縮式編碼 / 解碼(或自動編碼)、率下降和去噪擴散。
另一方面,該框架可以指導研究者推導或設計深度網絡架構,並且這些架構不僅在數學上是完全可解釋的,而且在大規模現實世界圖像或文本數據集上的幾乎所有學習任務上都能獲得頗具競爭力的性能。
基於以上觀察,他們提出一個白盒深度網絡理論。更具體而言,他們為學習緊湊和結構化的表征提出一個統一的目標,也就是一種有原理保證的優良度度量。對於學習到的表征,該目標旨在既優化其在編碼率下降方面的內在復雜性,也優化其在稀疏性方面的外在復雜性。他們將該目標稱為稀疏率下降(sparse rate reduction)。圖 3 給出這一目標背後的直觀思想。
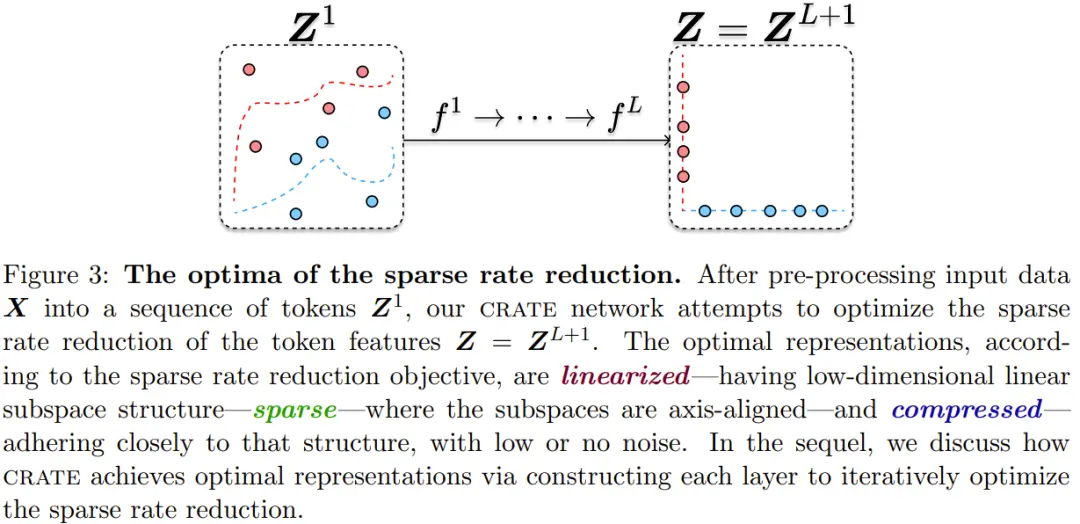
為優化這個目標,他們提出可以學習一個增量映射序列,其能模擬展開目標函數的某些類似梯度下降的迭代優化方案。這自然地會得到一個類似 Transformer 的深度網絡架構,並且它完全是一個“白盒”—— 其優化目標、網絡算子和學習到的表征在數學上是完全可解釋的。
他們將這個白盒深度架構命名為 CRATE 或 CRATE-Transformer,這是 Coding-RATE transformer 的縮寫。他們還通過數學方式證明這些增量映射在分佈的意義上是可逆的,並且它們的逆映射本質上由同一類數學算子構成。
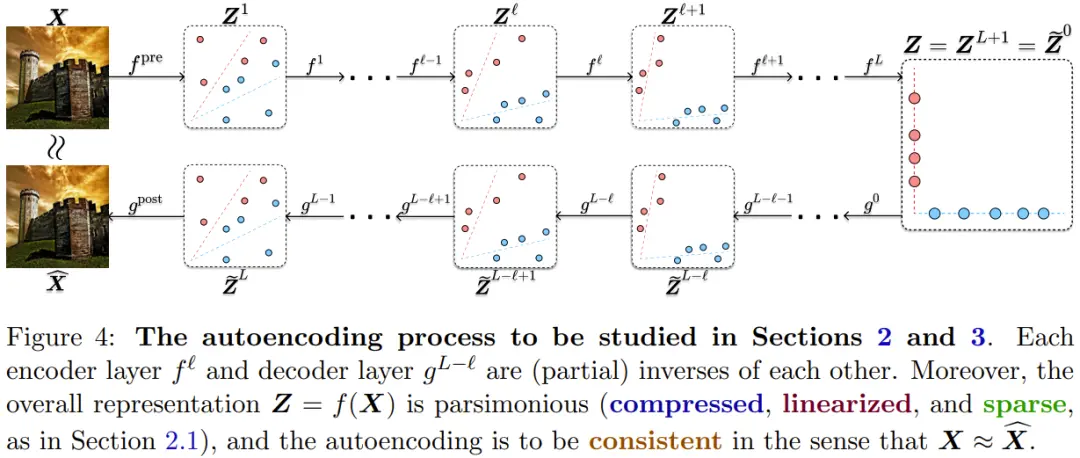
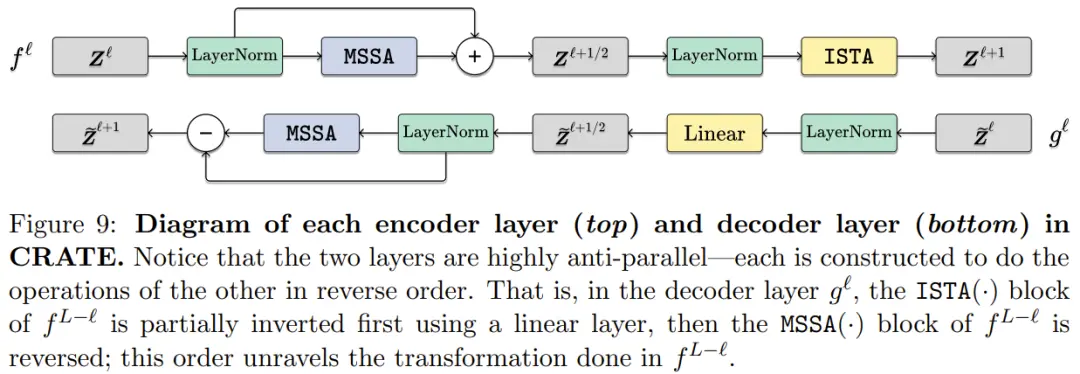
因此,可以將幾乎完全一樣的 CRATE 架構用於編碼器、解碼器或自動編碼器。如圖 4 給出一個自動編碼過程,其中每個編碼層 f^?? 和解碼層 g^{L-??} 是(部分)可逆的。
下圖給出 CRATE 白盒深度網絡設計的“主循環”。
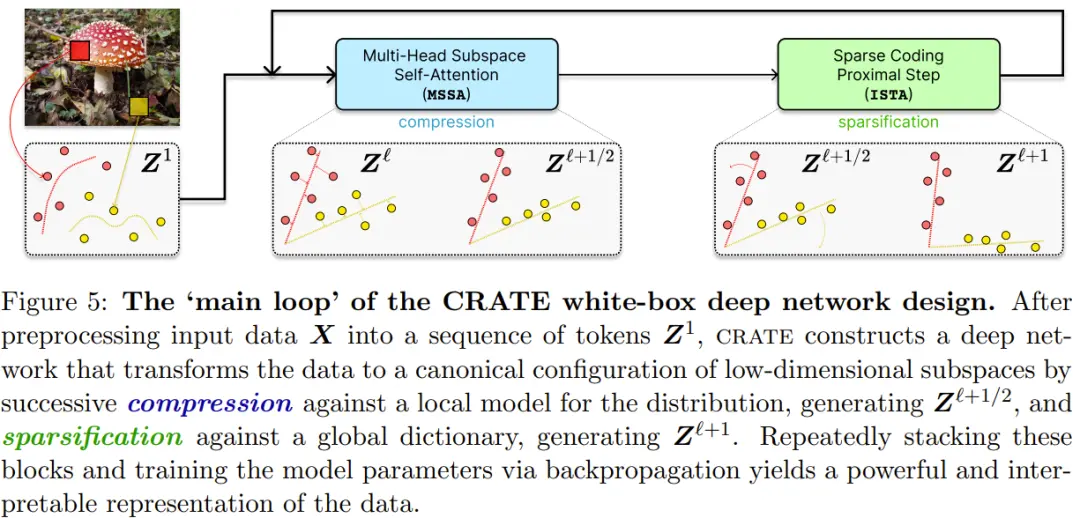
在將輸入數據 X 預處理為一系列 token Z^1 後,CRATE 會構建一個深度網絡,其可將數據轉換為低維子空間的規范配置,其做法是針對分佈的局部模型進行連續壓縮生成 Z^{?+1/2},以及針對一個全局詞典執行稀疏化,得到 Z^{?+1}。通過重復堆疊這些模塊並使用反向傳播訓練模型參數,可以得到強大且可解釋的數據表征。
下面則給出 CRATE 編碼器架構的一層。其完整架構就是將這些層串連起來,再加上一些初始 token 化器、預處理頭和最後的針對具體任務的頭。
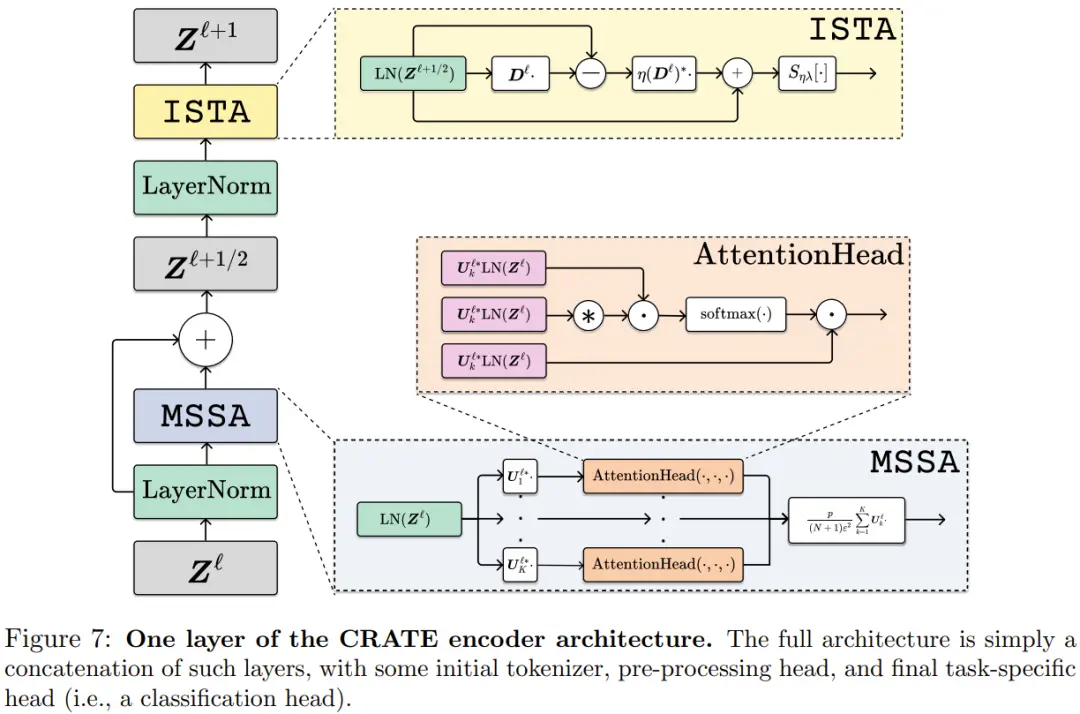
下圖對比編碼器層和解碼器層,可以看到兩者是部分可逆的。
更多理論和數學描述請參閱原論文。
實驗評估
為證明這個框架確實能將理論和實踐串連起來,他們在圖像和文本數據上執行廣泛的實驗,在傳統 Transformer 擅長的多種學習任務和設置上評估 CRATE 模型的實際性能。
下表給出不同大小的 CRATE 在不同數據集上的 Top-1 準確度。
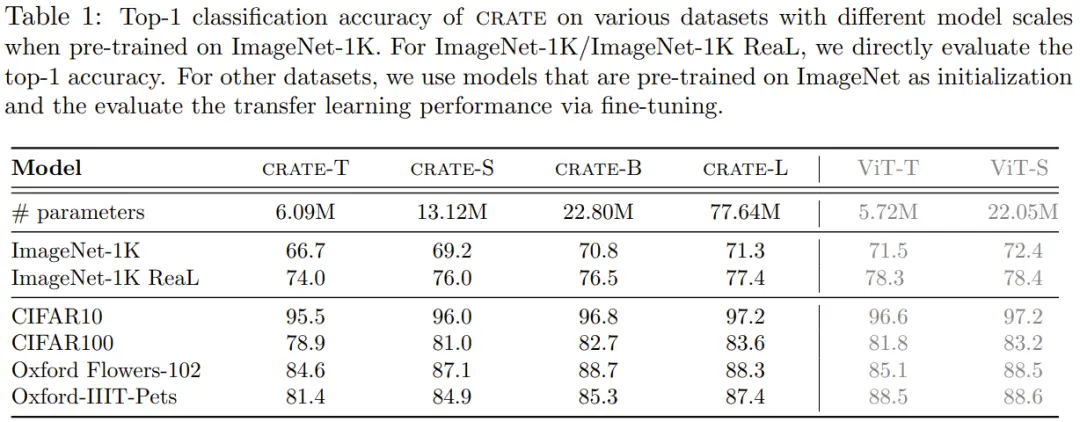
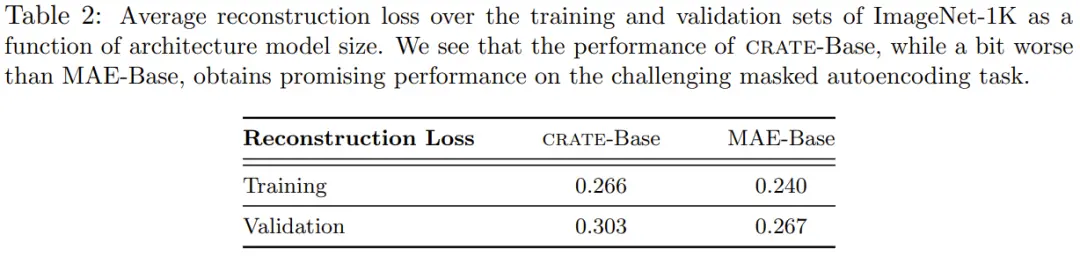
表 2 給出 CRATE-Base 模型與 MAE-Base 模型在訓練和驗證集上的平均重建損失。
令人驚訝的是,盡管其概念和結構很簡單,但CRATE 在所有任務和設置上都足以與黑盒版的對應方法媲美,這些任務包括通過監督學習進行圖像分類、圖像和語言的無監督掩碼補全、圖像數據的自監督特征學習、通過下一詞預測的語言建模。
此外,CRATE 模型在實踐上還有其它優勢,每一層和網絡算子都有統計和幾何意義、學習到的模型的可解釋性顯著優於黑盒模型、其特征具有語義含義(即它們可輕松用於將對象從背景中分割出來以及將其分成共享部件)。
下圖便給出在每層 ? 的逐層 token Z^? 表征的可視化。
下圖展示來自監督式 CRATE 的自註意力圖。

註意由於資源限制,他們在實驗中沒有刻意追求當前最佳,因為那需要大量工程開發或微調。
盡管如此,他們表示這些實驗已經令人信服地驗證新提出的白盒深度網絡 CRATE 模型是普遍有效的,並為進一步的工程開發和改進奠定堅實的基礎。