近日,來自MITFutureTech的研究人員發表一項關於大模型能力增長速度的研究,結果表明:LLM的能力大約每8個月就會翻一倍,速度遠超摩爾定律!我們人類可能要養不起AI!

論文地址:https://arxiv.org/pdf/2403.05812.pdf
LLM的能力提升大部分來自於算力,而摩爾定律代表著硬件算力的發展,
——也就是說,隨著時間的推移,終有一天我們將無法滿足LLM所需要的算力!
如果那個時候AI有意識,不知道會不會自己想辦法找飯吃?
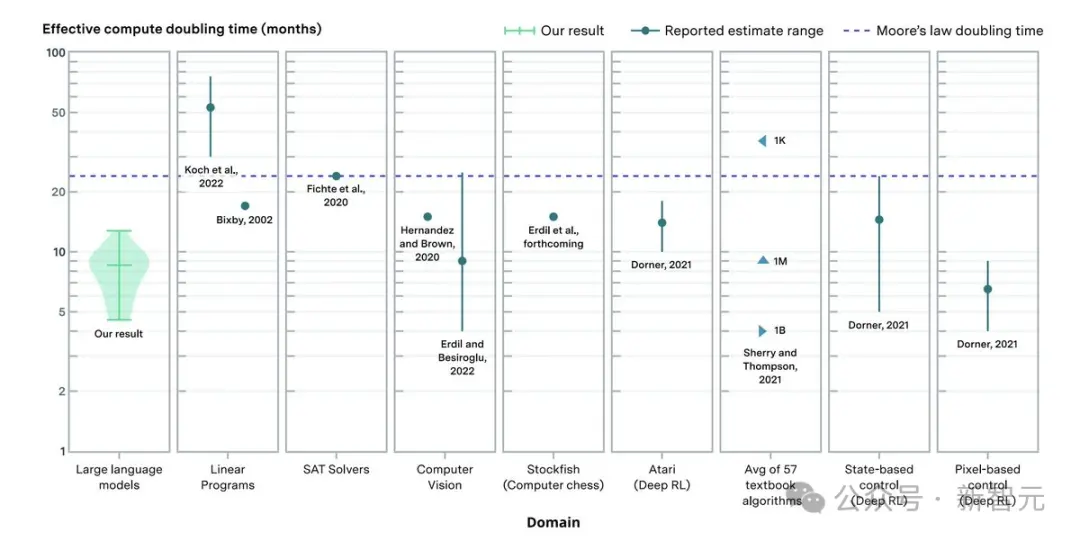
上圖表示不同領域的算法改進對有效計算翻倍的估計。 藍點表示中心估計值或范圍; 藍色三角形對應於不同大小(范圍從1K到1B)的問題的倍增時間; 紫色虛線對應於摩爾定律表示的2年倍增時間。
摩爾定律和比爾蓋茨
摩爾定律(Moore's law)是一種經驗或者觀察結果,表示集成電路(IC)中的晶體管數量大約每兩年翻一番。
1965年,仙童半導體(Fairchild Semiconductor)和英特爾的聯合創始人Gordon Moore假設集成電路的組件數量每年翻一番,並預測這種增長率將至少再持續十年。

1975年,展望下一個十年,他將預測修改為每兩年翻一番,復合年增長率(CAGR)為41%。
雖然Moore沒有使用經驗證據來預測歷史趨勢將繼續下去,但他的預測自1975年以來一直成立,所以也就成“定律”。
因為摩爾定律被半導體行業用於指導長期規劃和設定研發目標,所以在某種程度上,成一種自我實現預言。
數字電子技術的進步,例如微處理器價格的降低、內存容量(RAM 和閃存)的增加、傳感器的改進,甚至數碼相機中像素的數量和大小,都與摩爾定律密切相關。
數字電子的這些持續變化一直是技術和社會變革、生產力和經濟增長的驅動力。
不過光靠自我激勵肯定是不行的,雖然行業專傢沒法對摩爾定律能持續多久達成共識,但根據微處理器架構師的報告,自2010年左右以來,整個行業的半導體發展速度已經放緩,略低於摩爾定律預測的速度。
下面是維基百科給出的晶體管數量增長趨勢圖:
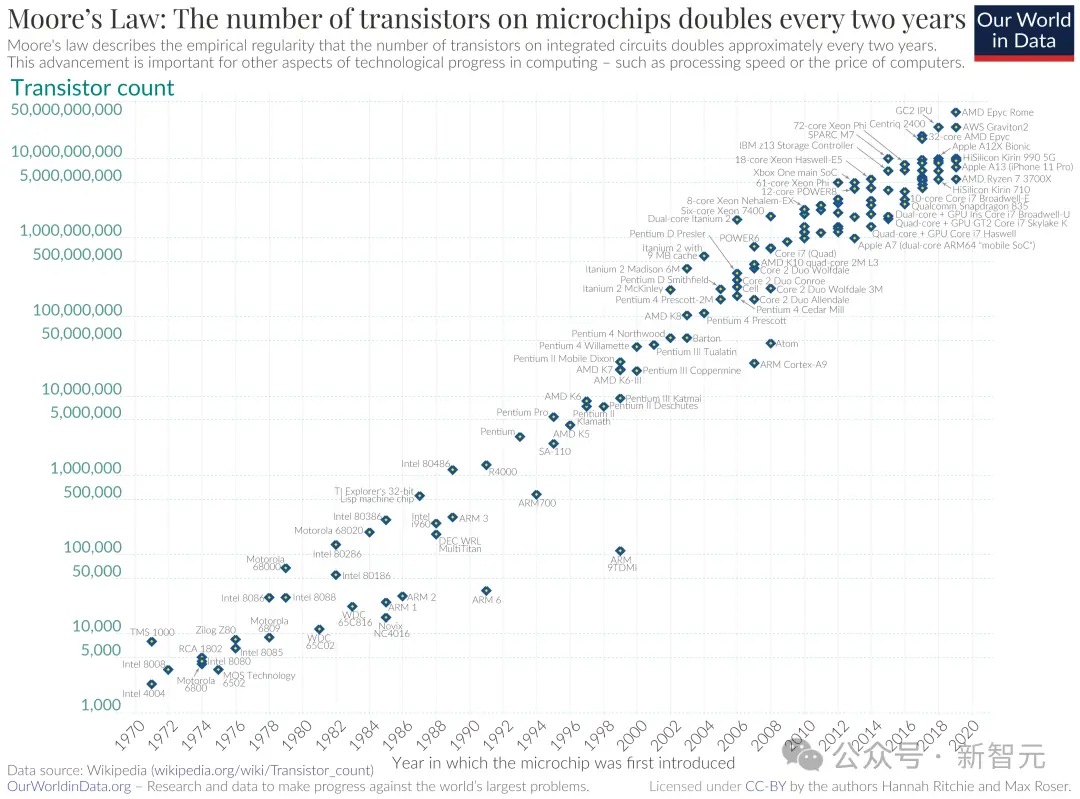
到2022年9月,英偉達首席執行官黃仁勛直言“摩爾定律已死”,不過英特爾首席執行官Pat Gelsinger則表示不同意。
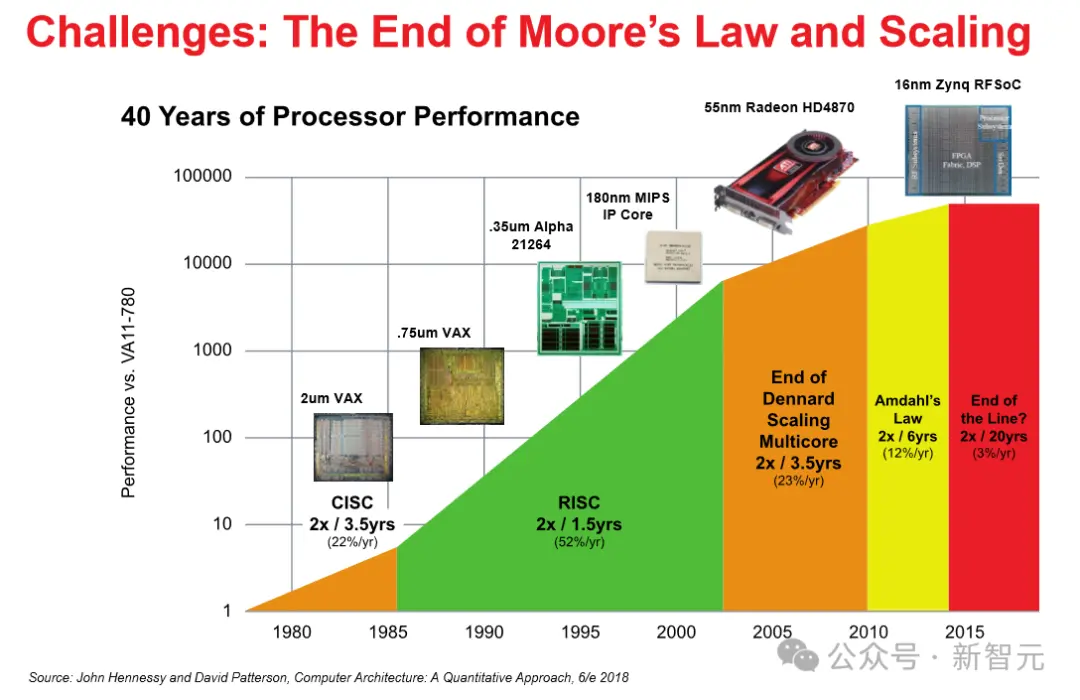
從下圖我們可以看出,英特爾還在努力用各種技術和方法為自己老祖宗提出的定律續命,並表示,問題不大,你看我們還是直線沒有彎。
Andy and Bill's Law
關於算力的增長,有一句話是這樣說的:“安迪給的,比爾都拿走(What Andy giveth, Bill taketh away)”。

這反映當時的英特爾首席執行官Andy Grove每次向市場推出新芯片時,微軟的CEO比爾·蓋茨(Bill Gates)都會通過升級軟件來吃掉芯片提升的性能。
——而以後吃掉芯片算力的就是大模型,而且根據MIT的這項研究,大模型以後根本吃不飽。
研究方法
如何定義LLM的能力提升?首先,研究人員對模型的能力進行量化。
基本的思想就是:如果一種算法或架構在基準測試中以一半的計算量獲得相同的結果,那麼就可以說,它比另一種算法或架構好兩倍。
有比賽規則之後,研究人員招募200多個語言模型來參加比賽,同時為確保公平公正,比賽所用的數據集是WikiText-103和WikiText-2以及Penn Treebank,代表多年來用於評估語言模型的高質量文本數據。
專註於語言模型開發過程中使用的既定基準,為比較新舊模型提供連續性。
需要註意的是,這裡隻量化預訓練模型的能力,沒有考慮一些“訓練後增強”手段,比如思維鏈提示(COT)、微調技術的改進或者集成搜索的方法(RAG)。
模型定義
研究人員通過擬合一個滿足兩個關鍵目標的模型來評估其性能水平:
(1)模型必須與之前關於神經標度定律的工作大致一致;
(2)模型應允許分解提高性能的主要因素,例如提高模型中數據或自由參數的使用效率。
這裡采用的核心方法類似於之前提出的縮放定律,將Dense Transformer的訓練損失L與其參數N的數量和訓練數據集大小D相關聯:
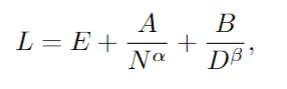
其中L是數據集上每個token的交叉熵損失,E、A、B、α和β是常數。E表示數據集的“不可減少損失”,而第二項和第三項分別代表由於模型或數據集的有限性而導致的錯誤。
因為隨著時間的推移,實現相同性能水平所需的資源(N 和 D)會減少。為衡量這一點,作者在模型中引入“有效數據”和“有效模型大小”的概念:
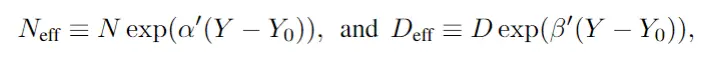
其中的Y表示年份,前面的系數表示進展率,代入上面的縮放定律,可以得到:
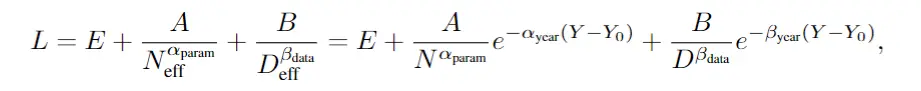
通過這個公式,就可以估計隨著時間的推移,實現相同性能水平所需的更少資源(N和D)的速度。
數據集
參與測評的包含400多個在WikiText-103(WT103)、WikiText-2(WT2)和Penn Treebank(PTB)上評估的語言模型,其中約60%可用於分析。
研究人員首先從大約200篇不同的論文中檢索相關的評估信息,又額外使用框架執行25個模型的評估。
然後,考慮數據的子集,其中包含擬合模型結構所需的信息:token級測試困惑度(決定交叉熵損失)、發佈日期、模型參數數量和訓練數據集大小,最終篩選出231個模型供分析。
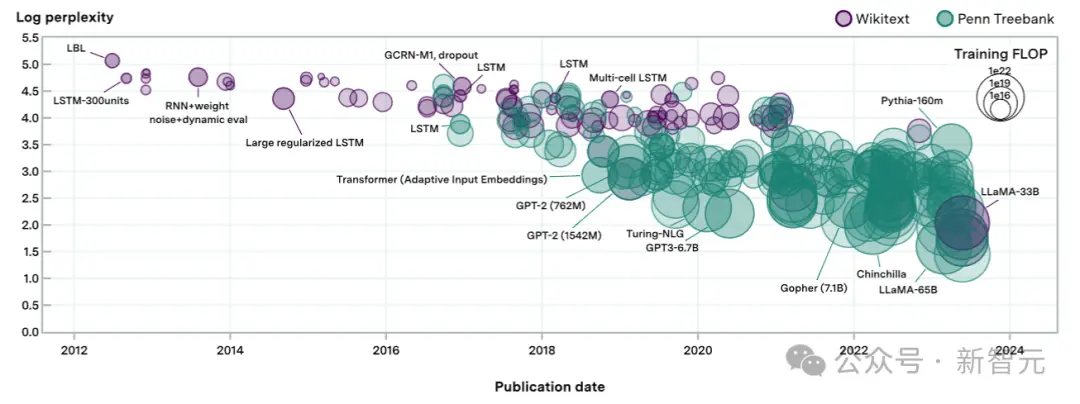
這231個語言模型,跨越超過8個數量級的計算,上圖中的每個形狀代表一個模型。
形狀的大小與訓練期間使用的計算成正比,困惑度評估來自於現有文獻以及作者自己的評估測試。
在某些情況下,會從同一篇論文中檢索到多個模型,為避免自相關帶來的問題,這裡每篇論文最多隻選擇三個模型。
實證結果
根據縮放定律,以及作者引入的有效數據、有效參數和有效計算的定義來進行評估,結果表明:有效計算的中位倍增時間為8.4個月,95%置信區間為4.5至14.3個月。
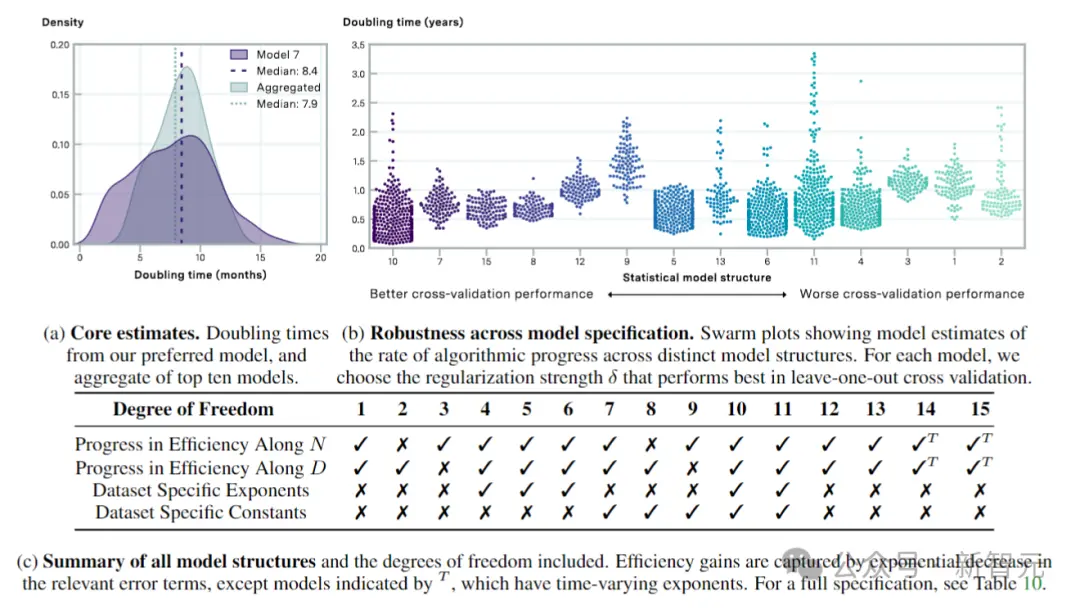
上圖表示通過交叉驗證選擇的模型的算法進度估計值。圖a顯示倍增時間的匯總估計值,圖b顯示從左到右按交叉驗證性能遞減(MSE測試損耗增加)排序。
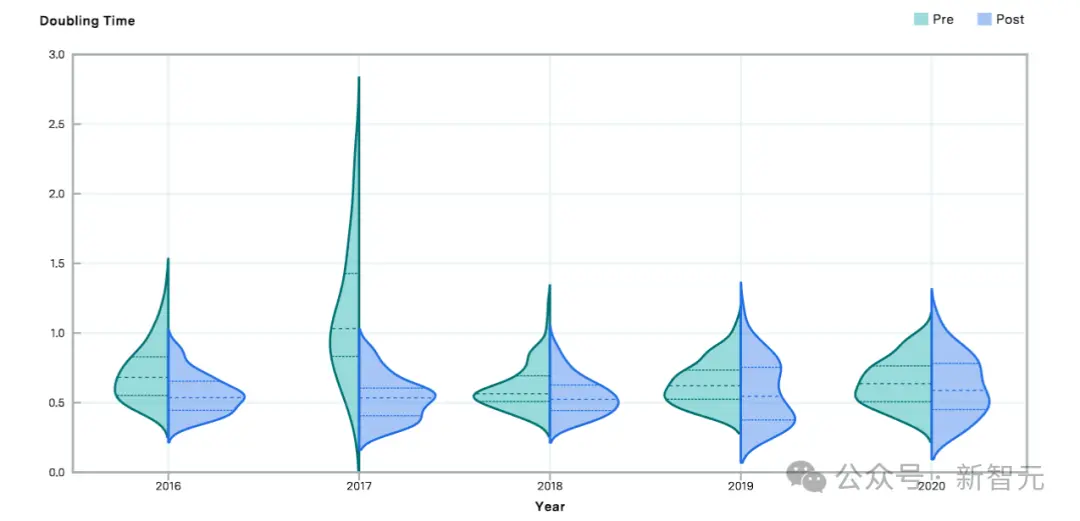
上圖比較2016年至2020年前後的算法有效計算的估計倍增時間。相對於前期,後期的倍增時間較短,表明在該截止年之後算法進步速度加快。
參考資料:
https://twitter.com/emollick/status/1767717692608217407