DeepMind碾壓人類高手的AI圍棋大師AlphaZero,下一個目標是數學算法!現已發現50年以來最快的矩陣乘法算法。下圍棋碾壓人類的AlphaZero,開始搞數學算法,先從矩陣乘法開始!
在昨天DeepMind團隊發表在Nature上的論文中,介紹 AlphaTensor,這是第一個用於為矩陣乘法等基本計算任務發現新穎、高效、正確算法的AI系統。

論文鏈接:
https://www.nature.com/articles/s41586-022-05172-4.pdf
AlphaTensor為一個 50 年來的懸而未決的數學問題找到新答案:找到兩個矩陣相乘的最快方法。
先看看這研究都說的啥。
提高基礎計算算法的效率一直都是學界熱點,因為它會影響大量計算的整體速度,從而對智能計算領域產生多米諾骨牌式的效應。
上一張圖,來看看AlphaTensor有多“能幹”。
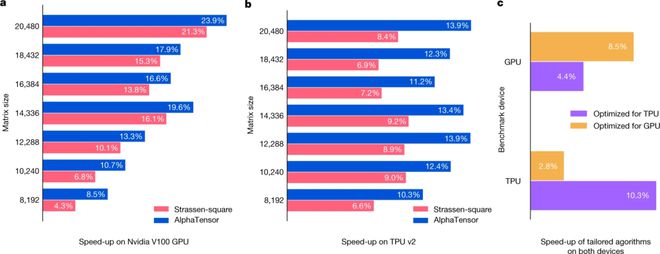
圖a,b為AlphaTensor發現的算法在GPU (a) 和 TPU (b)上的加速百分比表現,針對大小為 8,192 × 8,192的矩陣乘法進行優化
矩陣乘法就是這樣一項原始任務,從神經網絡到科學計算程序,它都是不可或缺的部分。
然而,算法發現過程的自動化是復雜的,因為可能的算法空間是巨大的。
DeepMind這次發佈一種基於AlphaZero的深度強化學習方法,用於發現任意矩陣乘法的有效且可證明正確的算法。
這個算法空間包含標準矩陣乘法算法和遞歸算法。
DeepMind將矩陣乘法算法發現過程(即張量分解問題)制定為一個單人遊戲——TensorGame。
AlphaTensor 建立在 AlphaZero 之上,訓練一個神經網絡來指導規劃過程,以搜索有效的矩陣乘法算法。

我們的框架使用單個智能體來分解各種大小的矩陣乘法張量,從而產生跨各種張量的學習分解技術的轉移。為解決遊戲的挑戰性,AlphaTensor 使用專門的神經網絡架構,利用問題的對稱性並利用合成訓練遊戲。
AlphaTensor可擴展到比人工或組合搜索所能達到的算法空間大得多的算法空間。
事實上,AlphaTensor 從零開始發現許多可證明正確的矩陣乘法算法,這些算法在標量乘法的數量方面改進現有算法。
結果表明,AlphaTensor發現的算法在許多矩陣規模上都優於最先進的方法。
從圍棋到矩陣乘法:AlphaZero“出圈”
矩陣乘法,學過線性代數的都熟悉,作為矩陣變換的基礎運算之一,矩陣乘法是 線性代數 的基礎工具,不僅在數學中有大量應用,在 應用數學 、 物理學 、 工程學 等領域也有廣泛使用。
作為構成數學算法的基礎運算之一,矩陣乘法的應用史長達數千年。
早在古埃及時代,人們就創造一種無需乘法表的兩個數字相乘的算法,希臘數學傢歐幾裡德描述一種計算最大公約數的算法,這種算法至今仍在使用。

在伊斯蘭黃金時代,波斯數學傢Muhammad ibn Musa al-Khwarizmi設計新的算法來解決線性和二次方程。事實上,al-Khwarizmi的名字被翻譯成拉丁文為Algoritmi,這就是今天英文“算法”一詞的前身。
但是,盡管今天人們對算法非常熟悉,但是,發現新算法的過程是非常困難的。
在我們今天發表在《自然》雜志上的論文中,我們介紹AlphaTensor,這是第一個用於發現新的、高效的、可證明正確的矩陣乘法等基本任務算法的AI系統。這為數學領域一個長達50年的開放性問題——如何尋找兩個矩陣相乘的最快方法——給出答案。
這是DeepMind推動科學發展和利用AI解開最基本問題的又一次實踐。AlphaTensor建立在AlphaZero的基礎上,後者是一個在國際象棋、圍棋和象棋等棋類遊戲上表現超出人類的智能體,從下棋,到解決半個世紀以來的數學算法,AlphaZero是如何做到的?
打破矩陣乘法50年最快記錄
矩陣乘法是代數中最簡單的操作之一,通常在高中數學課上教授。 但在課堂之外,這個不起眼的數學運算在當代數字世界有著巨大的影響力,在現代計算機中無處不在。
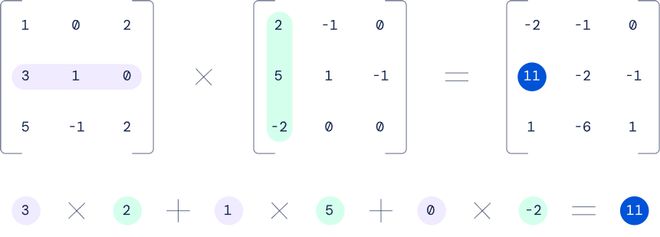
3*3矩陣相乘的計算
矩陣乘法被用於處理智能手機上的圖像,識別語音命令,為計算機遊戲生成圖形,運行模擬以預測天氣,壓縮數據和視頻以在互聯網上共享等,應用極為廣泛。
世界各地的公司花費大量的時間和金錢來開發計算硬件,以有效地進行矩陣乘法。因此,即使是對矩陣乘法效率的微小改進也會產生廣泛的影響。
幾個世紀以來,數學傢們認為,標準的矩陣乘法算法是人們在效率方面所能達到的最佳狀態。

但在1969年,德國數學傢Volken Strassen震驚數學界,他表明確實存在更好的算法。

此前的矩陣乘法的標準算法與Strassen的算法相比,後者在乘2x2矩陣時少用一個標量乘法(7次而不是8次)。就整體計算效率而言,乘法比加法重要得多。
通過研究非常小的矩陣(大小為2x2),他發現一種巧妙的方法來組合矩陣的條目,從而產生一種更快的算法。盡管經過幾十年的研究,這個問題的更大版本仍然沒有得到解決--以至於人們不知道如何有效地將兩個小到3x3的矩陣相乘。
在Nature的新論文中,我們探討現代人工智能技術如何推進新矩陣乘法算法的自動發現。AlphaTensor發現在許多矩陣大小上比現有技術水平更有效的算法。我們的人工智能設計的算法優於人類設計的算法,這是在算法發現領域的一個重大進步。
AI推動算法發現的自動化
首先,我們將尋找矩陣乘法的有效算法問題轉化為一個單人遊戲。 在這個遊戲中,棋盤是一個三維張量(數字陣列),記錄當前算法離正確的程度。
通過一組與算法指令相對應的允許移動,玩傢試圖修改張量並將其條目清零。當玩傢成功做到這一點時,對於任何一對矩陣來說,都會產生一個可證明正確的矩陣乘法算法,而其效率則由將張量清零所需的步驟數來體現。
這個遊戲具有令人難以置信的挑戰性--要考慮的可能算法的數量遠遠大於宇宙中的原子數量,即使是對於矩陣乘法的小案例。與幾十年來一直是人工智能挑戰的圍棋遊戲相比,我們的遊戲每一步可能的動作數量要大30個數量級。
從本質上講,要玩好這個遊戲,相當於要在“巨大的幹草堆中找出最小的那根針”。
為應對這個明顯不同於傳統遊戲的領域的挑戰,我們開發多個關鍵組件,包括一個新的神經網絡架構,其中包括特定問題的歸納偏見,一個生成有用的合成數據的程序,以及一個利用問題的對稱性的配方。
然後,我們利用強化學習訓練一個AlphaTensor智能體來玩一個單人遊戲(Tensor Game),開始時沒有任何關於現有矩陣乘法算法的知識。
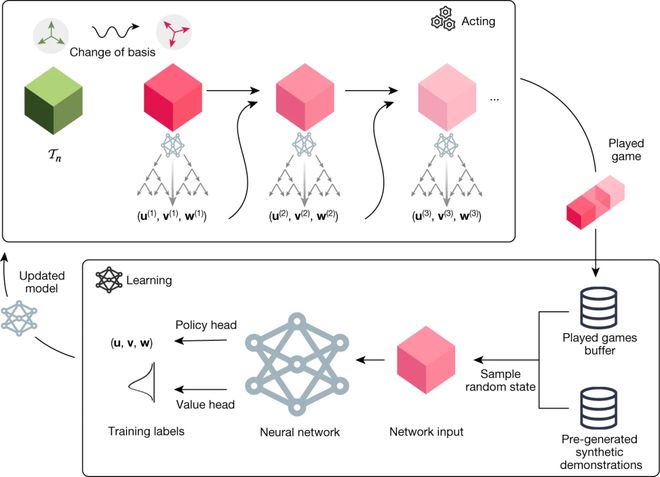
AlphaTensor在TensorGame中的目標則是在有限因子空間內找到張量分解 (Tensor Decomposition)。
在介紹張量分解之前,我們可能需要先簡單地解一下張量是什麼,然後再考慮張量分解有什麼用途。
從初中到大學,我們接觸最多的可能隻是標量(scalar)、向量(vector)和矩陣(matrix),而張量則不那麼常見,但實際上,標量是第0階張量,向量是第1階張量,矩陣是第2階張量,第3階或階數更高的張量被稱為高階張量(higher-order tensor),一般提到的張量都是特指高階張量。
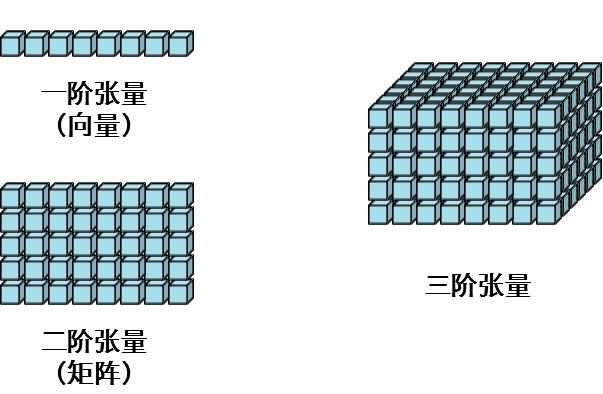
我們也知道,在一個矩陣中,某一元素的位置可以說成“第幾行第幾列”的形式,要表達某一元素的位置需要兩個索引構成的組合 ,類似地,在一個第3階張量裡面,表達某一元素的位置需要三個索引構成的組合 。
在處理稀疏矩陣和稀疏張量時,用索引來標記元素的位置會帶來很多便利。另外,階數的張量可以理解為矩陣的維泛化,在這裡,階數其實就是空間維度(spatial dimension),張量可以被視為多維數組。
張量分解從本質上來說是矩陣分解的高階泛化。
對矩陣分解有所解的讀者可能知道,矩陣分解有三個很明顯的用途,即降維處理、缺失數據填補和隱性關系挖掘,而張量分解也能夠很好地滿足這些用途。
為解決TensorGame並找到有效的矩陣乘法算法,我們開發一個DRL智能體AlphaTensor。
通過學習,AlphaTensor隨著時間的推移逐漸改進,重新發現歷史上的快速矩陣乘法算法,如Strassen的算法,最終超越人類的直覺領域,發現的算法比以前已知的更快。
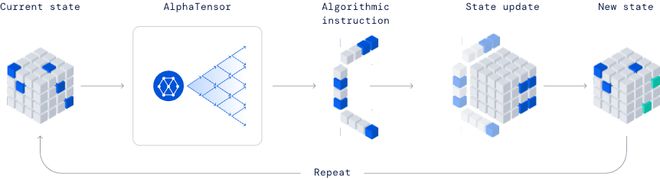
由AlphaTensor玩的單人遊戲,目標是找到一個正確的矩陣乘法算法。遊戲的狀態是一個由數字組成的立方體數組(顯示為灰色為0,藍色為1,綠色為-1),代表著要做的剩餘工作。
例如,如果學校裡教的傳統算法是用100次乘法對一個4x5乘以5x5的矩陣進行乘法,而這個數字在人類的聰明才智下被減少到80次,AlphaTensor已經找到隻用76次乘法就能完成同樣操作的算法。
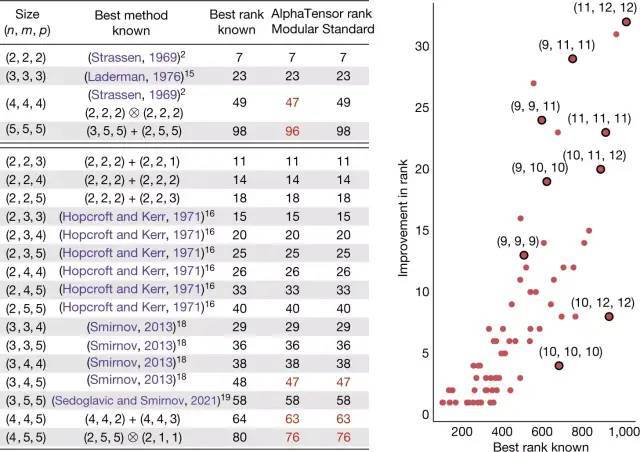
除此之外,AlphaTensor的算法自50年前發現以來,首次在有限域中改進Strassen的兩級算法。這些小矩陣的乘法算法可以作為基元來乘以任意大小的大得多的矩陣。
此外,AlphaTensor還發現一組具有最先進復雜度的多樣化算法--每種大小的矩陣乘法算法多達數千種,表明矩陣乘法算法的空間比以前想象的要豐富。
在這個豐富的空間中的算法具有不同的數學和實踐屬性。利用這種多樣性,我們對AlphaTensor進行調整,以專門尋找在特定硬件上速度快的算法,如NVIDIA V100 GPU,和GoogleTPU v2。
這些算法在相同的硬件上比常用的算法快10-20%,這展示AlphaTensor在優化任意目標上的靈活性。
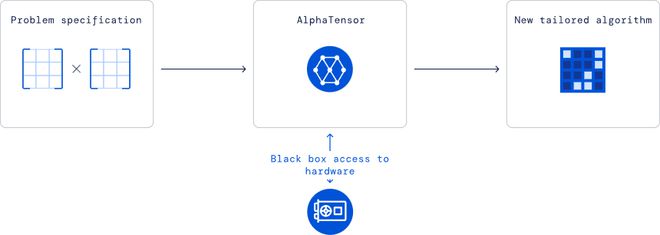
AlphaTensor的目標是對應於算法的運行時間。當發現一個正確的矩陣乘法算法時,會在目標硬件上進行基準測試,然後反饋給AlphaTensor,以便在目標硬件上學習更有效的算法。
未來的研究和應用
從數學的角度來看,我們的結果可以指導復雜性理論的進一步研究,其目的是確定解決計算問題的最快算法。
通過以比以前的方法更有效的方式探索可能的算法空間,AlphaTensor有助於推進我們對矩陣乘法算法的豐富性的理解。解這個空間可能會釋放出新的結果,幫助確定矩陣乘法的漸進復雜性,這是計算機科學中最基本的開放問題之一。
因為矩陣乘法是許多計算任務的核心組成部分,涵蓋計算機圖形、數字通信、神經網絡訓練和科學計算,AlphaTensor發現的算法可以使這些領域的計算效率大大提升。
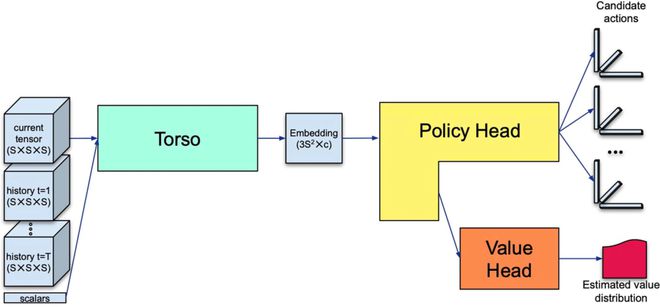
圖為AlphaTensor網絡架構
AlphaTensor在考慮任何類型的目標方面的靈活性也可以刺激新的應用,以設計優化能源使用和數值穩定性等指標的算法,幫助防止小的四舍五入錯誤隨著算法的工作而滾雪球。
雖然我們在這裡集中討論矩陣乘法這一特殊問題,但我們希望我們的論文能夠啟發其他人使用人工智能來指導其他基本計算任務的算法發現。
我們的研究還表明,AlphaZero是一個強大的算法,可以遠遠超出傳統遊戲的領域,幫助解決數學中的開放問題。
在我們的研究基礎上,我們希望能夠推動更多的工作--應用人工智能來幫助社會解決數學和整個科學領域的一些最重要的挑戰。
參考資料:
https://www.nature.com/articles/s41586-022-05172-4
https://www.newscientist.com/article/2340343-deepmind-ai-finds-new-way-to-multiply-numbers-and-speed-up-computers/